Systematic random sampling

Systematic random sampling is a type of probability sampling technique [see our article Probability sampling if you do not know what probability sampling is]. With the systematic random sample, there is an equal chance (probability) of selecting each unit from within the population when creating the sample. The systematic sample is a variation on the simple random sample. Rather than referring to random number tables to select the cases that will be included in your sample, you select units directly from the sample frame [see our article, Sampling: The basics, if you are unsure about the terms unit, sample, sampling frame and population]. This article explains (a) what systematic random sampling is, (b) how to create a systematic random sample, and (c) the advantages and disadvantages (limitations) of systematic random sampling.

Systematic random sampling explained

Imagine that a researcher wants to understand more about the career goals of students at the University of Bath. Let's say that the university has roughly 10,000 students. These 10,000 students are our population (N). In order to select a sample (n) of students from this population of 10,000 students, we could choose to use a systematic random sample.

With systematic random sampling, there would an equal chance (probability) that each of the 10,000 students could be selected for inclusion in our sample. Each of the 10,000 students is known as a unit, a case or an object (these terms are sometimes used interchangeably; we use the word unit). If our desired sample size was around 400 students, each of these students would subsequently be sent a questionnaire to complete (imagining we choose to collect our data using a questionnaire).

Creating a simple random sample

To create a systemic random sample, there are seven steps: (a) defining the population; (b) choosing your sample size; (c) listing the population; (d) assigning numbers to cases; (e) calculating the sampling fraction; (f) selecting the first unit; and (g) selecting your sample.

STEP ONE
Define the population

In our example, the population is the 10,000 students at the University of Bath. The population is expressed as N. Since we are interested in all of these university students, we can say that our sampling frame is all 10,000 students. If we were only interested in female university students, for example, we would exclude all males in creating our sampling frame, which would be much less than 10,000.

STEP TWO
Choose your sample size

Let's imagine that we choose a sample size of 100 students. The sample is expressed as n. This number was chosen because it reflects the limit of our budget and the time we have to distribute our questionnaire to students. However, we could have also determined the sample size we needed using a sample size calculation, which is a particularly useful statistical tool. This may have suggested that we needed a larger sample size; perhaps as many as 400 students.

STEP THREE
List the population

To select a sample of 100 students, we need to identify all 10,000 students at the University of Bath. If you were actually carrying out this research, you would most likely have had to receive permission from Student Records (or another department in the university) to view a list of all students studying at the university. You can read about this later in the article under Disadvantages (limitations) of systematic random sampling.

STEP FOUR
Assign numbers to cases

We now need to assign a consecutive number from 1 to N, next to each of the students. In our case, this would mean assigning a consecutive number from 1 to 10,000 (i.e. N = 10,000; your population of students at the university).

STEP FIVE
Calculate the sampling fraction

Assuming we have chosen a sample size of 100 students, we now need to work out the sampling fraction, which is simply the sample size selected (expressed as n) divided by the population size (N). In this case:

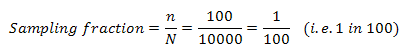
The sampling fraction tells us that we need to select 1 student in every 100 students from the population of 10,000 students at the university. After doing this 100 times, we will have our sample of 100 students. However, first we need to select the first unit (i.e., the first student), which starts the process of creating our sample.

STEP SIX
Select the first unit

Since we need to select 1 student in every 100 students, first we use a random number table to select the first student. Imagine the first number in the random number table was 0009, we would ignore the first three digits and focus on the last digit, 9, since this number fits between 0 and 100. As such, our first student would be the 9th on our list of 10,000 students.

STEP SEVEN
Select your sample

Now that we know the first unit, namely the 9th student on the list, we can select the other 99 students to make up our sample of 100 students. Since we need to select 1 student in every 100 students from the list, we use the 9th student as the starting point and then select every 100th student from this point. As such, we select the 109th student on the list, the 209th student, the 309th student, and so forth.

Advantages and disadvantages (limitations) of systematic random sampling

The advantages and disadvantages (limitations) of systematic random sampling are explained below. Many of these are similar to other types of probability sampling technique, but with some exceptions. Whilst systematic random sampling is one of the "gold standards" of sampling techniques, it presents many challenges for students conducting dissertation research at the undergraduate and master's level.